In this part, I first implement a UNet for one-step denoising. Then, I add time-conditioning and finally class conditioning with CFG.
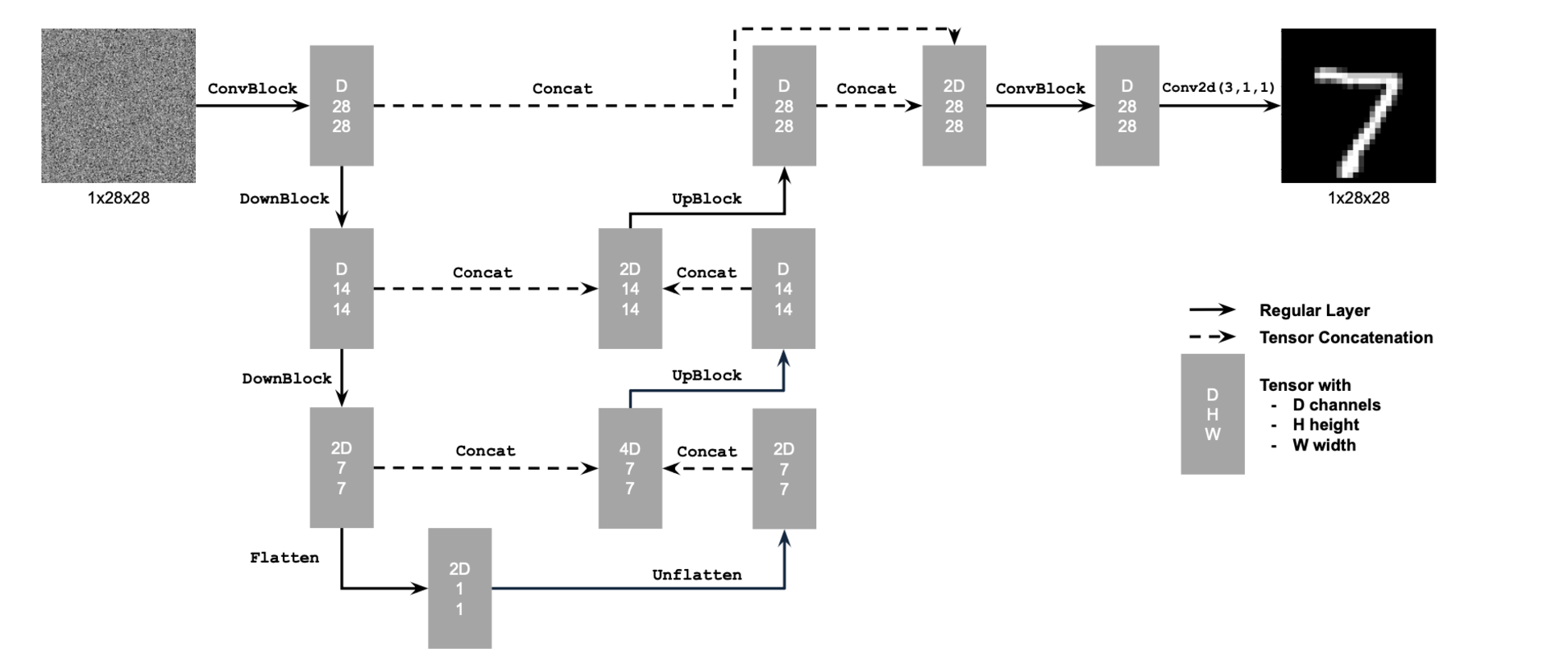
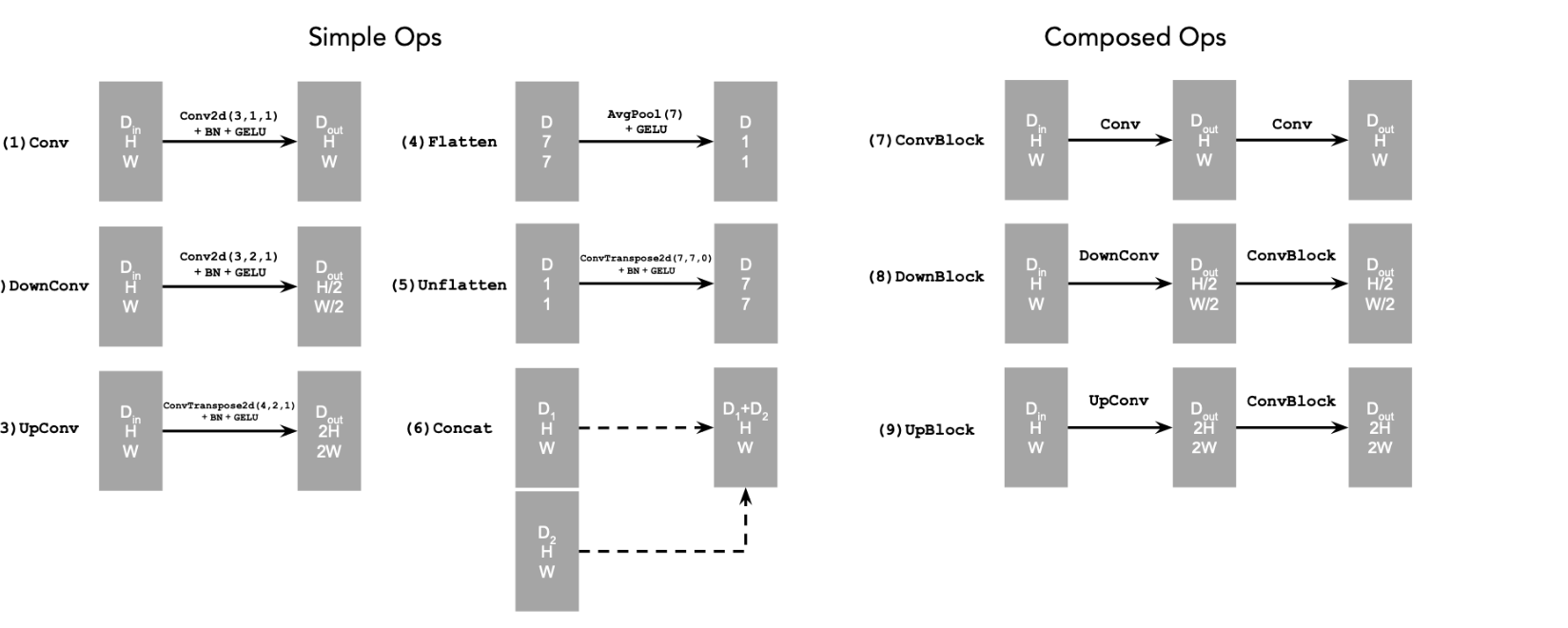
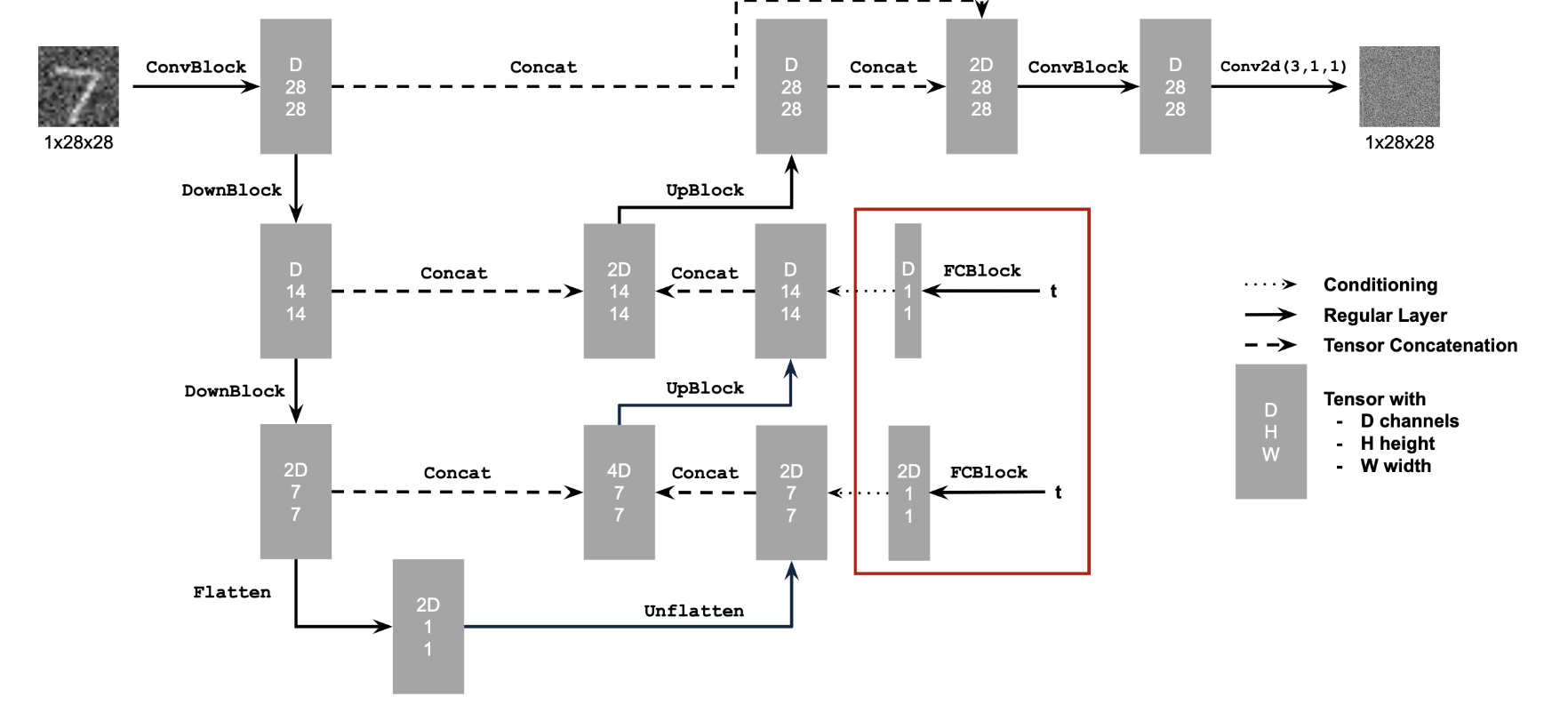
Implementing a UNet from scratch! I implemented this using the following UNet architecture and operations.


We define the loss function to be the L2 loss between the denoied image and the clean image. To create noised images for training, I added gaussian noise of different degrees to MNIST images.

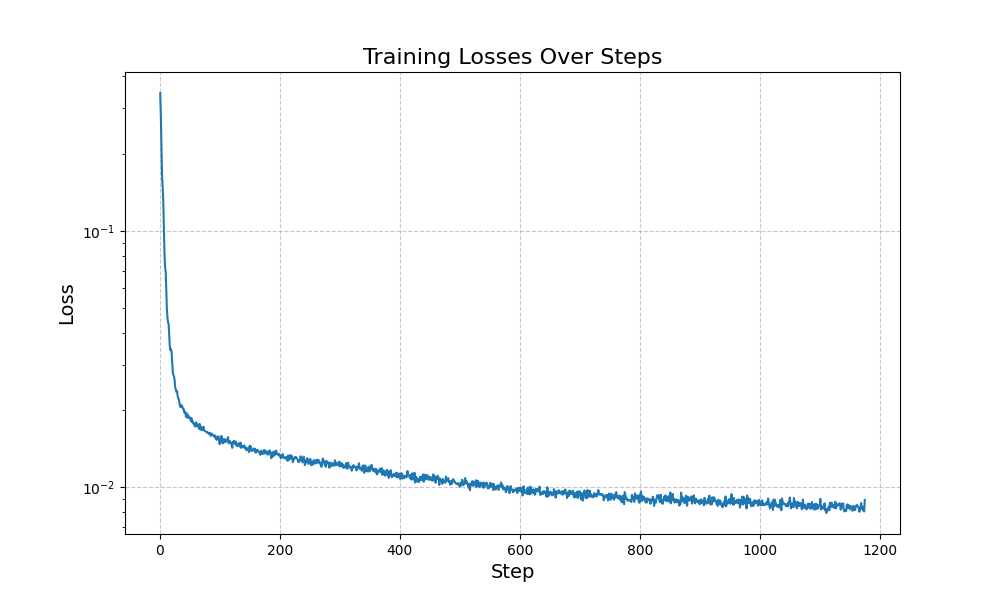
The following shows the one-step denoising training for noise at the level sigma = 0.5. The batch size was 256, run for 5 epochs, with a learning rate of 1e-4.
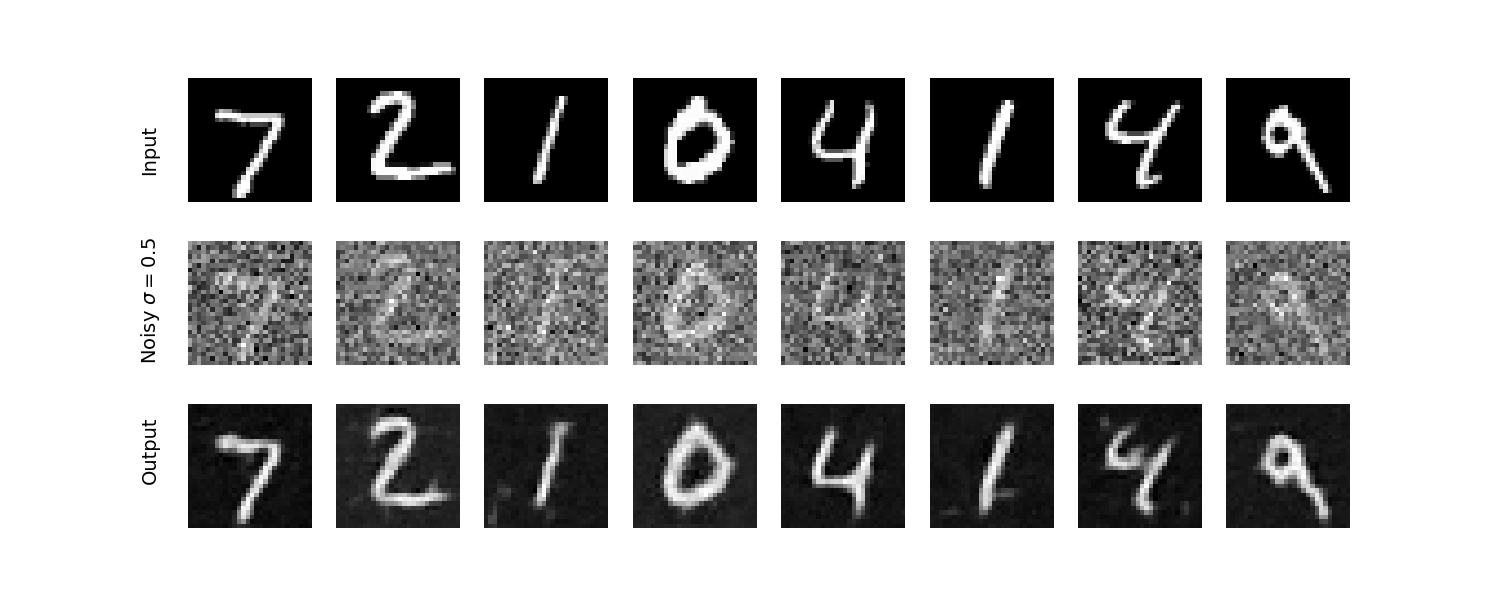
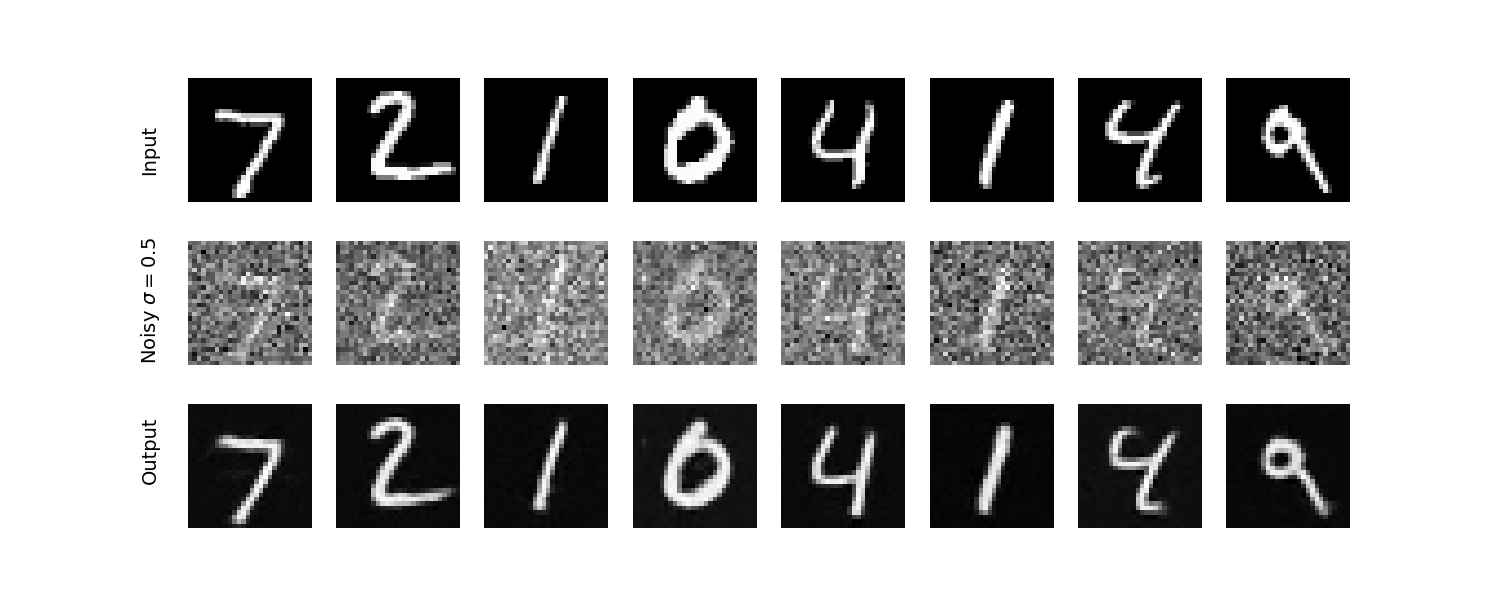
Here is how the one-step denoising UNet performs for an image it was not trained on (from the test set)

Instead of just predicting the clean image all at once (which we saw even in Part A was not that great), we can instead predict the noise at each step. To do this, we'll change the objective function to be the L2 loss between the predicted noise at a time step and the actual noise. Architecure wise, we need to add a FullyConnectedBlock to add the timestep into the model.
Here is the algorithm that was used for training:

For training, I used a batch size of 128 and trained for 20 epochs.
Here is the algorithm that was used for sampling:



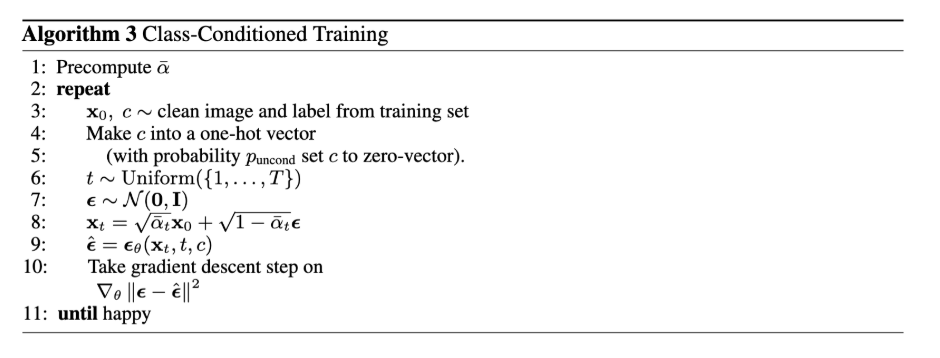
But wait! What if I wanted to guide the model to generate specific digits (similar to prompt embeddings for part A)? To do this, we one-hot encoded a class-conditioning vector, c to represent the different 10 classes (digits). We use a dropout of 10% for the conditioning so that it still doesn't need to have conditioning. Trained for 20 epochs. Here is the algorithm for training:
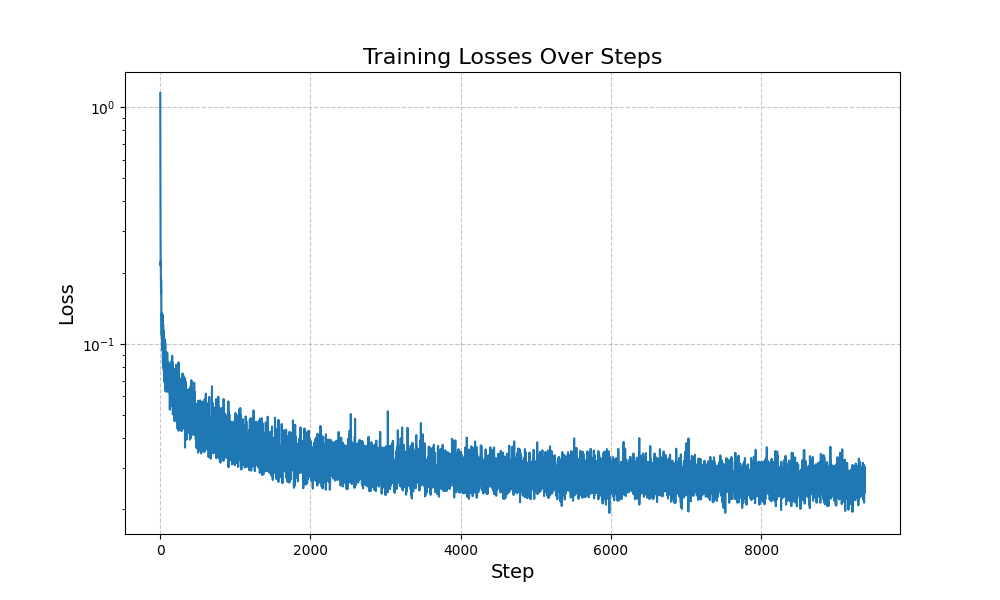
Here, we implement CFG, using unconditioned and conditioned passes through the model. Gamma was set to 5.0 and here is the sampling at the following epochs. Here is the algorithm for sampling:


